具有高散热性能的陶瓷基板用于大功率电子设备，本文主要研究活性材料钎焊（AMB）陶瓷基板制造过程中产生的翘曲变形和残余应力。为了基板设计提供重要的参数，并确保良好的可靠性。在有限元用于分析陶瓷、金属和焊料厚度、陶瓷基板尺寸和压力对残余应力分布和翘曲变形的影响。

比较了热弹性和热弹塑性有限元的计算结果，在焊接过程中的塑性变形过程极大地影响计算结果的准确性，发现最大轴向应力集中在陶瓷侧，轴向残余应力是引起陶瓷基体开裂的主要因素。陶瓷、金属和焊料的厚度以及基板尺寸对残余应力有显着影响和翘曲变形，在这两者都可以通过施加外部压力来减少。

与传统的塑料基印刷电路板相比，陶瓷基板具有更好的导热性。陶瓷基板与较厚的金属层相结合，可用于在极端环境下运行的大功率电子设备。常用的陶瓷材料有AIN、AI2O3和Si3N4。具有170W/mk的高导热率的AIN基板，提供了一个很好的替代传统的24W/mk的氧化铝（AI2O3）基板，以实现更好的散热。然而，AlN衬底(α= 4.3 ppm/℃)仍然存在与铜(α= 16.3 ppm/℃)不匹配的高热膨胀系数(CTE)。活性材料钎焊（AMB）陶瓷基板是直接键合铜（DBC）的进一步发展，它基于陶瓷和活性元素在高温下的反应。因此，AMB陶瓷基板具有更高的结合力和可靠性。

冷却过程中陶瓷金属界面处会产生残余应力，由于CTE不匹配残余应力值受以下因素影响很多因素。残余应力对陶瓷金属有很大影响界面性能。较大的变形导致蚀刻减少精度，而较高的残余应力会降低抗疲劳性和使用寿命。因此，在控制基板变形和减少残余应力对提高精度和使用性能具有重要意义。

确定薄膜残余应力的最常用方法是基于在基板方面的基板弯曲变形曲率半径。薄膜中的残余应力可以使用计算斯托尼方程：

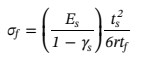
其中，Es和γs分别是杨氏模量和泊松比基材，ts和tf分别代表基板和薄膜的厚度。该公式的准确条件之一是薄膜比基材薄得多。然而，在本文中金属层厚度与陶瓷基板的厚度比较接近，在冷却过程中金属会发生塑性变形。当基板的厚度接近薄膜时，或在残余应力作用下的结构发生较大变形时，都会影响残余应力结果的准确性。在这里残余应力是使用有限元法(FEM)计算的，以确保结果的准确性。

由于材料的厚度是可变的，因此不应使用曲率半径来测量界面处的应力。热的残余应力可以用方程式表示，这不需要考虑材料厚度：

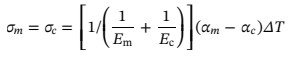
其中，Em是金属的弹性模量，Ec是金属的弹性模量陶瓷，αm是金属的热膨胀系数，αc是陶瓷的热膨胀系数，ΔT是从高到低的冷却间隔。该公式只计算了弹性范围内的接头热残余应力，没有考虑材料性能随温度的变化，因此计算结果存在较大偏差。

有限元法已被广泛用于预测残差钎焊连接处的应力，然而关于AMB陶瓷基板残余应力和变形的研究尚未有结果，在采用有限元分析方法分析了影响不锈钢板翅结构残余应力的因素。结果表明，材料失配。钎焊间隙、压力载荷、翅片间距、厚度和高度，以及板厚显着影响残差应力分布。研究表明钎焊的Si3N4/42CrMo接头的热应力分布活性填料，结果表明，在峰值拉伸轴向残余应力总是出现在Si3N4陶瓷中。现已经有很多文章研究下DBC陶瓷基板的应力变化循环加热条件。对直接镀铜(DPC)氮化铝(AlN)进行了有限元研究基质，它也是从经过验证的有限元模拟中发现的铜膜楔角、长度和厚度显着影响热循环加载过程中AlN的最大第一主应力。

在本文中，陶瓷金属和焊料厚度的影响。随着陶瓷基板尺寸和残余应力压力和钎焊过程中产生的翘曲变形分析如下：有限元分析的下，该研究有助于控制生产过程中的残余应力和变形。目前，在残余应力和变形的计算通常通过数值模拟来实现。在仿真过程中，陶瓷基板可以不受机械约束地自由翘曲。本文研究旨在了解陶瓷基板残余热应力的形成机理，掌握其变形规律及主要影响因素。

一、有限元模型

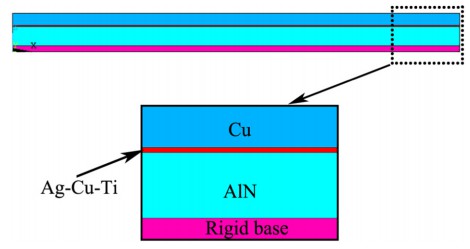
基于热弹塑性应力应变行为并考虑材料特性随温度的变化，ANSYS用于分析AMB陶瓷基板的残余应力和变形。该模型为单面陶瓷基板，如图1所示，以10 °C/min的速度将样品从 800 °C 冷却至室温冷却速度。不考虑反应层分析，因为它太薄，相变的影响是忽略。假设冷却过程中的样品温度是均匀的，具有完美的界面附着力。此外，计算中没有考虑界面强化的影响。采用 von-Mises 屈服准则，等效应力为：

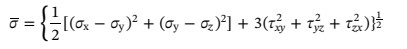
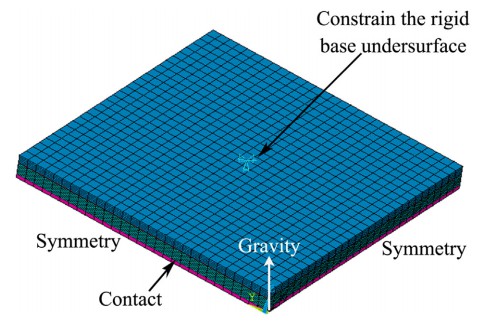
模型采用3D弹塑性有限元分析方法。使用8节点对模型进行网格划分，在模拟中过程中，对模型施加的约束如图2所示。将样品和刚性底座设置为接触对，使样品可以自由弯曲。采用1/4对称模型来简化有限元计算。

二、残余应力和翘曲结果

1、热弹性和热塑性有限元的比较

本文对热弹性有限元的计算结果将热弹塑性有限元法与热弹塑性有限元法进行比较，热弹塑性有限元法计算的结果更接近实际测量结果。在这个模型中，陶瓷的厚度是0.635毫米，铜金属层的厚度为0.3毫米，厚度为Ag-Cu-Ti 焊料层为 50 μm。样品的变形为用数显高度计测量，如图3所示。如果塑料不考虑焊接过程的变形，可靠性计算量会大大减少。但是，计算结果热弹塑性有限元模型更适合实际

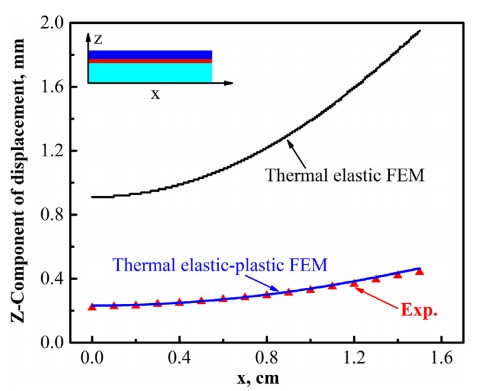
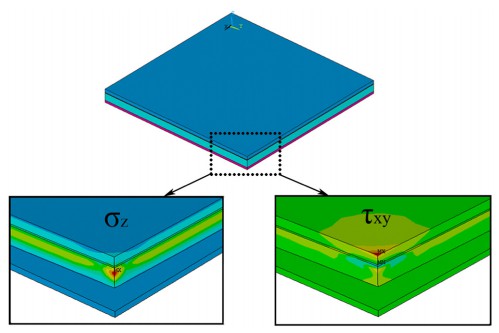
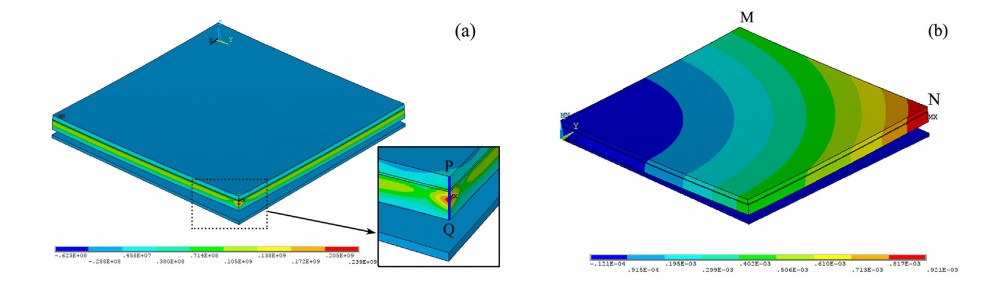
本文对热弹性有限元的计算结果将热弹塑性有限元法与热弹塑性有限元法进行比较，热弹塑性有限元法计算的结果更接近实际测量结果。在这个模型中，陶瓷的厚度是0.635毫米，铜金属层的厚度为0.3毫米，厚度为Ag-Cu-Ti焊料层为50 μm。样品的变形为用数显高度计测量，如图3所示。如果塑料不考虑焊接过程的变形，可靠性计算量会大大减少。但是计算结果热弹塑性有限元模型更适合实际情况和计算是可靠的。根据调查结果如图4拐角区域试样的剪应力计算和轴向残余应力图可知，轴向拉伸应力是陶瓷基板失效的主要因素。

 2、陶瓷厚度对翘曲和残余应力的影响

不仅影响轴向残余应力和翘曲变形，由材料的热膨胀系数和尺寸决定的基板。不同陶瓷厚度的有限元模型模拟揭示了陶瓷厚度对翘曲变形和残余应力的有影响。铜膜厚度为0.3mm，Ag-Cu-Ti填充金属层为50μm，面积为陶瓷基板保持不变。轴向残余应力和陶瓷基板的翘曲变形图，厚度为0.635mm如图5a和图5b所示。从轴向残差应力图，最大轴向应力集中在陶瓷上边。可不同陶瓷沿PQ路径的σz分布厚度如图6a所示。可以看出来，陶瓷厚度变化对最大σz有很大影响。

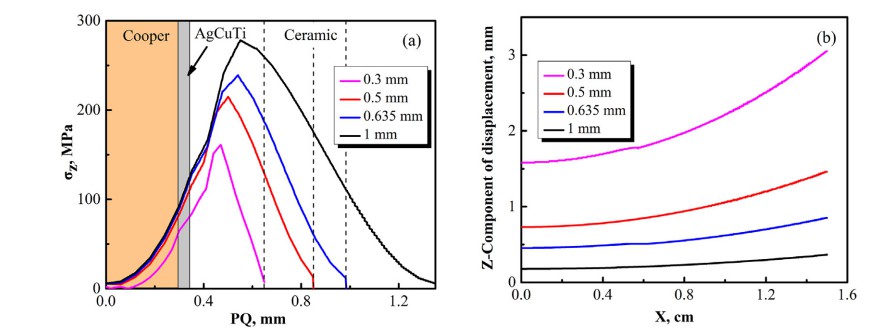
当陶瓷厚度增加，残余应力分布保持不变基本不变，但峰值应力增加。很明显陶瓷厚度越大，轴向应力越大。此外，可以看出轴向应力是拉伸的，如图6b所示陶瓷厚度与z分量的关系。沿MN路径的位移，需要注意X定义为长度从M到N，表明随着陶瓷厚度的增加，整体翘曲逐渐减小。从图6(a)和图6(b)可以看出，对应陶瓷厚度的最大轴向残余应力0.3mm、0.5mm、0.635mm和1mm分别为161 MPa、215 MPa、239 MPa和278兆帕。分别对应陶瓷厚度0.3 mm、0.5 mm、0.635 mm和1 mm的最大轴向位移分别为3.165毫米、1.47毫米、0.922毫米和0.376毫米。什么时候陶瓷厚度为0.3 mm，变形最大，相应陶瓷基板的轴向应力最小。

3、铜层厚度对翘曲和残余应力的影响

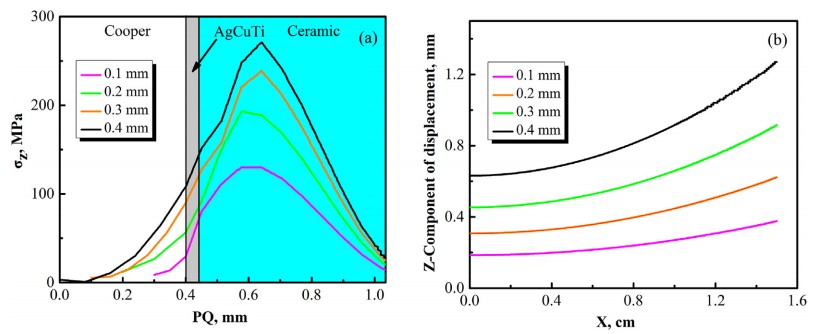
陶瓷基板的铜层厚度是一个重要参数，这对翘曲变形和轴向残余应力很重要发展。为了研究铜层厚度效应，四种FEM型号，带0.1 mm、0.2 mm、0.3 mm 和 0.4 mm铜厚度被开发出来。轴向残余应力分布PQ 路径和沿 MN 路径位移的Z分量不同铜层厚度的陶瓷基板如图所示图7(a)和图7(b)。表明轴向残余应力增加铜厚。铜层厚度0.1 mm、0.2 mm、0.3 mm和0.3 mm 对应的最大轴向残余应力0.4 mm分别为 140 MPa、200 MPa、239 MPa和271 MPa。这铜层厚度0.1mm、0.2mm、0.3mm、0.4mm对应的最大轴向位移为0.207mm、0.626mm，

分别为 0.922毫米和1.277毫米。对于0.1毫米厚的铜层，陶瓷基板的变形梯度很小，从而减少残余应力。随着金属厚度的增加，沿PQ路径的残余轴向应力的总体趋势没有改变显着，但应力峰值增加。

4、焊料厚度对翘曲和残余应力的影响

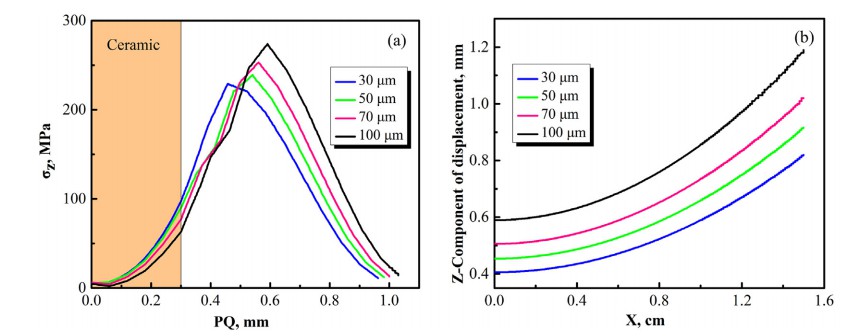
在本节中，设计了四个模型来研究焊料层厚度对翘曲变形和残余应力的影响AMB陶瓷基板：30 μm、50 μm、70 μm和100 μm。焊料层厚度对沿PQ路径和Z分量的轴向应力的影响沿MN路径的位移如图8所示。轴向应力随焊料层厚度增加。最大轴向残差对应于30 μm、50 μm、70 μm 焊料厚度的应力100 μm分别为229 MPa、239 MPa、253 MPa和278 MPa。焊料厚度对应的最大轴向位移30 μm、50 μm、70 μm 和 100 μm 分别为 0.826 mm、0.922 mm、1.026 mm和 1.193 毫米分别。

5、基板尺寸对翘曲和残余应力的影响

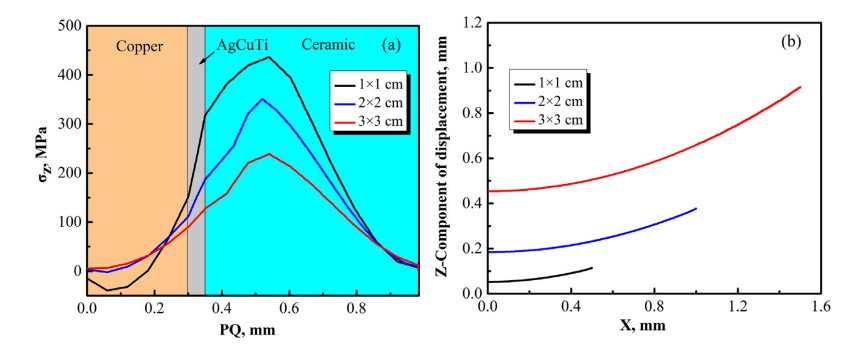
通过考虑基板的尺寸进行了类似的分析，如图9所示。当基板的尺寸从1 × 1 cm到2 × 2 cm和 3 × 3 cm，翘曲变形增加。然而，轴向残余应力随着增加而减小基板尺寸。对应的最大轴向残余应力为1 × 1 cm、2 × 2 cm和3 × 3 cm尺寸分别为 436 MPa、350 MPa和分别为 239 兆帕。对应的最大轴向位移到1 × 1 厘米、 2 × 2厘米和3 × 3厘米大小是0.114毫米、 0.377 毫米和分别为0.922毫米。随着样本量的减小，趋势残余应力分布发生了变化。对于1 cm × 1 c的样品，沿PQ路径的轴向残余应力分布不完全是拉伸的，它从拉伸变为压缩从界面。

6、压力对翘曲变形和残余应力的影响

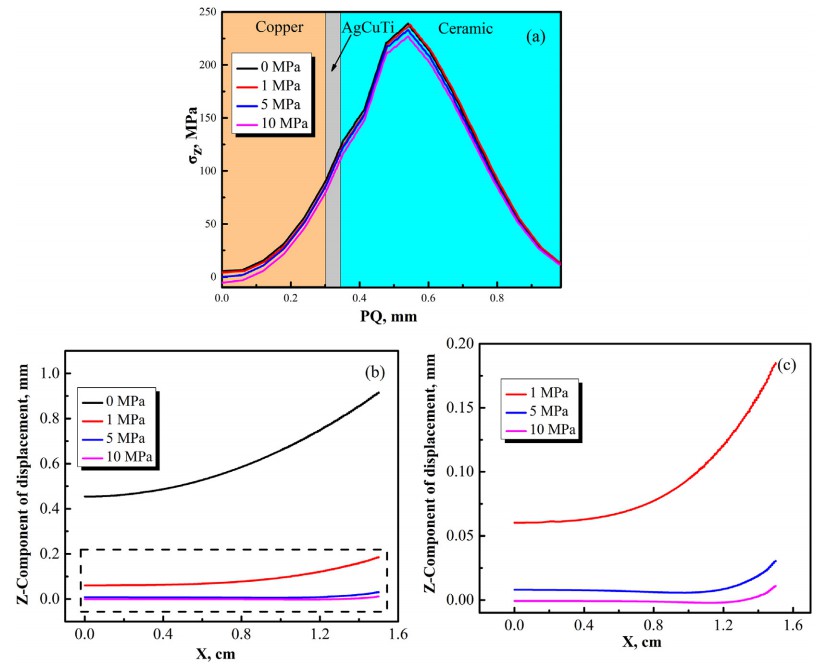
热应力的产生是一个积累的过程，界面的轴向残余应力和翘曲变形可通过在AMB陶瓷基板上施加一定的压力来减少钎焊过程中，结果如图9所示。随着钎焊压力，轴向残余应力的分布趋势为基本不变，但施加的压力越大，释放界面的轴向残余应力。当压力为1 MPa时，界面处的应力与未施加压力时相同。然而，在 10 MPa 基底压力下，轴向残余应力降低到227 MPa。同时，压力不宜过大，否则会导致陶瓷破裂和焊料溢出。图10(a)显示了沿 PQ 路径的 σz 分布，适用于不同的压力基板。图10（b）显示了Z分量沿MN路径和图10（c）显示了放大的区域。